问题
填空题
设函数f(x)在(-∞，+∞)上可导，f(1)=1，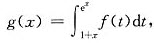
则g’’(0)=（）。
答案
参考答案：1．
解析：
由变限定积分的求导公式，有
g’(x)=exf(ex)-f(1+x)，
g’’(x)=exf’(ex)+exf(ex)-f’(1+x)，可知
g’’(0)=f’(1)+f(1)-f’(1)=1．
搜题请搜索小程序“爱下问搜题”
设函数f(x)在(-∞，+∞)上可导，f(1)=1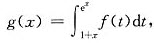，则g’’(0)=（）。
参考答案：1．
解析：
由变限定积分的求导公式，有
g’(x)=exf(ex)-f(1+x)，
g’’(x)=exf’(ex)+exf(ex)-f’(1+x)，可知
g’’(0)=f’(1)+f(1)-f’(1)=1．