问题
问答题
设函数f(x)
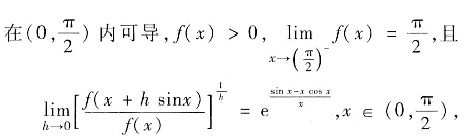
(Ⅰ) 求f(x)的表达式； (Ⅱ) 证明函数f(x)在
有界．
答案
参考答案：(Ⅰ)
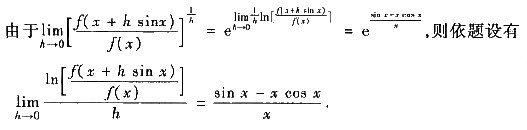
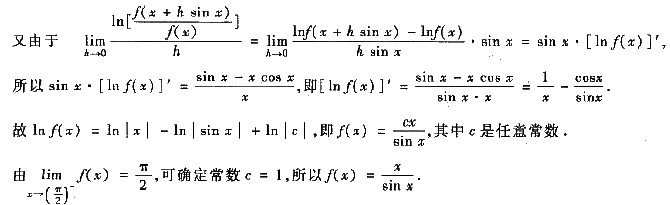
(Ⅱ)
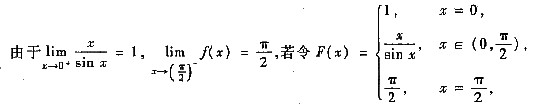
则F(x)在
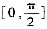上连续，根据闭区间上连续函数的性质可得：F(x)在
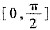上有界，从而F(x)在
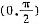内有界，又当
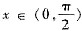时f(x)=F(x)，所以f(x)在
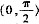有界．
搜题请搜索小程序“爱下问搜题”
设函数f(x)
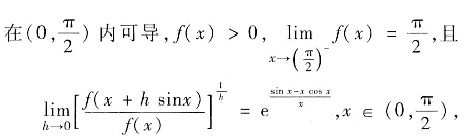
(Ⅰ) 求f(x)的表达式； (Ⅱ) 证明函数f(x)在
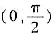有界．
参考答案：(Ⅰ)
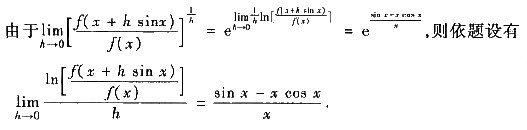
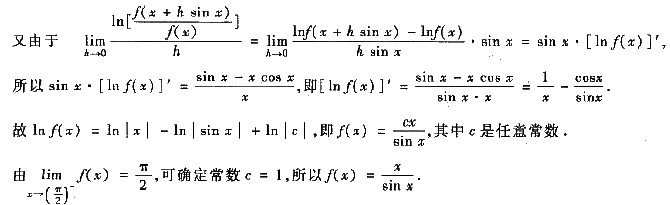
(Ⅱ)
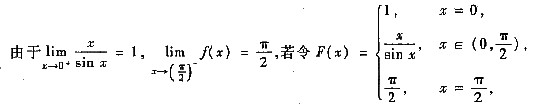
则F(x)在
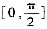上连续，根据闭区间上连续函数的性质可得：F(x)在
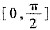上有界，从而F(x)在
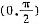内有界，又当
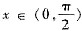时f(x)=F(x)，所以f(x)在
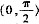有界．