问题
问答题
设函数f(x)对于[a，b]上任意两点x1与x2恒有|f(x1)-f(x2)|≤q|x1-x2|(其中q为常数)，且f(A) f(B) ＜0，证明：至少存在一点ξ∈(a，b)，使得f(ξ)=0．
答案
参考答案：[证] 因为任意两点x1与x2恒有|f(x1)-f(x2)|≤q|x1-x2|，所以
|f(x+△x)-f(x)|≤q|△x|．
由夹逼定理可得：
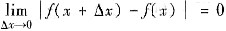，从而
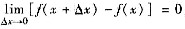，所以f(x)在[a，b]上连续．又f(A) f(B) ＜0，故南零点定理可得：至少存在一点ξ∈(a，b)，使得f(ξ)=0．