问题
单项选择题
下列命题正确的是
(A) 若f(x)在点x0处连续，g(x)在点x0处不连续，则f(x)+g(x)在点x0处可能连续．
(B) 若f(x)在点x0处连续，则
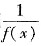在点x0处也连续．
(C) 若f(x)在点x0处连续，则f(x)在点x0处也连续．
(D) 若|f(x)|在点x0处连续，则f(x)在点x0处也连续．
答案
参考答案：C
解析： (A)显然不成立，若f(x)+g(x)在点x0处连续，因为[f(x)+g(x)]-f(x)=g(x)，由连续函数的性质知g(x)在点x0处连续．
(B)也应排除，这是因为f(x0)可能为零．
(D)不正确，例如f(x)
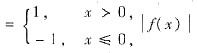在x=0处连续，而f(x)在x=0处间断．
(C)是正确的，因为不等式||f(x)|-|f(x0)||≤|f(x)-f(x0)|总成立，故可由f(x)在点x=x0处的连续性推出|f(x)|必在点x=x0处连续．故应选(C)．
[评注] 由本题可知，“f(x)在点x0处连续”是“|f(x)|在点x0处连续”的充分但非必要条件．