问题
单项选择题
下列命题正确的是
(A) 设f(x)定义在(-∞，+∞)，若
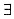c，f(x)在(-∞，c]和(c，+∞)上均连续，则f(x)在(-∞，+∞)上连续．
(B) 若f(x)在x=x0连续，则
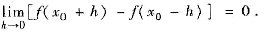
(C) 若f(x)在x=x0连续，g(x)在x=x0不连续，则f(x)g(x)在x=x0不连续．
(D) 若
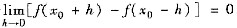，则f(x)在x=x0连续．
答案
参考答案：B
解析： 利用f(x)在点x=x0处连续的定义可得
故应选(B)．
对于(A)：若令x0=c，则所给条件仅表明f(x)在x0左连续，不能保证在x0右连续．如
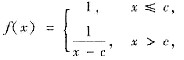
显然f(x)在(-∞，c]连续(在点x=c处是左连续)，在(c，+∞)也连续，但在点x=c处不连续，
因为
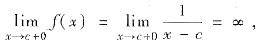
因此(A)不正确．
对于(C)：
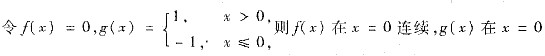不连续，而f(x)g(x)在x=0处连续，所以(C)不正确．
对于
，而f(x)在x=x0=0不连续，所以(D)也不正确．