[背景材料]
已知网络计划图如图7-2所示,箭线下方括号外数字为工作的正常持续时间,括号内数字为工作的最短持续时间;箭线上方括号外数字为正常持续时间时的直接费,括号内数字为最短持续时间时的直接费。费用单位为千元,时间单位为天。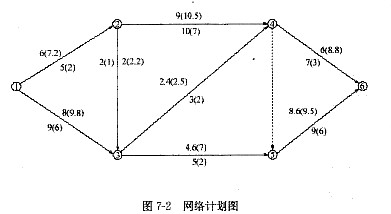
[问题]
如果工程间接费率为0.8千元/天,则最低工程费用时的工期为多少天
参考答案:
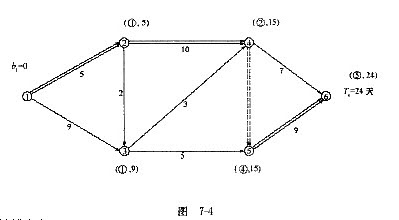
(1)用标号法确定网络计划的计算工期和关键线路,如图7-4所示。计算工期Tc=24天。
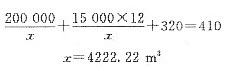
键线路为:1—2—4—5—6。
(2)计算各项工作的直接费率:

 (3)计算工程总费用:
(3)计算工程总费用:
1)直接费总和:Cd=(6.0+8.0+2.0+9.0+2.4+4.6+6.0+8.6)千元=46.6千元
2)间接费总和:Ci=O.8×24千元=19.2千元
3)工程总费用:Ct=Cd+Ci=(46.6+19.2)千元=65.8千元
(4)通过压缩关键工作的持续时间进行费用优化:
1)第一次压缩:
由图7-4可知,有以下3个压缩方案:①压缩工作1—2,直接费用率为0.4千元/天。②压缩工作2—4,直接费用率为0.5千元/天。③压缩工作5—6,直接费用率为0.3千元/天。上述三种压缩方案中,由于工作5—6的直接费用率最小,且小于间接费用率,故应选择工作5—6作为压缩对象。
将工作5—6的持续时间压缩3天,这时工作5—6将变成非关键工作,故将其压缩2天,使其恢复为关键工作。第一次压缩后的网络计划图如图7-5所示。用标号法计算网络计划的计算工期为Tc=22天,图7-5中的关键线路有两条,即:1—2—4—5—6和1—2—4—6。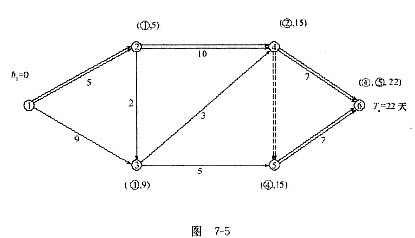
2)第二次压缩:
从图7-5可知,有以下3种压缩方案:①压缩工作1—2,直接费用率为0.4千元/天;②压缩工作2—4,直接费用率为O.5千元/天;③同时压缩工作4—6和工作5—6,组合直接费用率为:(0.7+0.3)千元/天=1.0千元/天。故应选择直接费用率最小且小于间接费用率的工作1—2作为压缩对象。
将工作1—2的持续时间压缩至最短(即2天),将会使工作1—2变成非关键工作,同时,将工作1—2的持续时间压缩至3天,也会使其变成非关键工作,故只能将工作1—2压缩1天。压缩后用标号法计算网络计划时间参数如图7-6所示。即计算工期Tc=21天,关键线路有三条:1—2—4—6和1—2—4—5—6及1—3—5—6。
3)第三次压缩:
从图7-6可知,有以下7种压缩方案:①同时压缩工作1—2和工作1—3,组合直接费用率为1.O千元/天。②同时压缩工作1—2和工作3—5,组合直接费用率为1.2千元/天。③同时压缩工作1—2和工作5—6,组合直接费用率O.7干元/天。④同时压缩工作2—4与工作1—3,组合直接费用率为1.1千元/天。⑤同时压缩工作2—4和工作3—5,组合直接费用率为1.3千元/天。⑥同时压缩工作2—4和工作5—6,组合直接费用率为0.8千元/天。⑦同时压缩工作4—6和工作5—6,组合直接费用率为1.O千元/天。上述7种压缩方案中,方案③即同时压缩工作1—2和工作5—6,组合直接费用率最小,且小于间接费用率,故选择此方案。
将工作1—2和工作5—6的持续时间同时压缩1天,压缩后它们仍然是关键工作,故可行。压缩后用标号法计算网络计划时间参数如图7-7所示。即计算工期Tc=20天,关键线路有两条:1—2—4—6和1—3—5—6。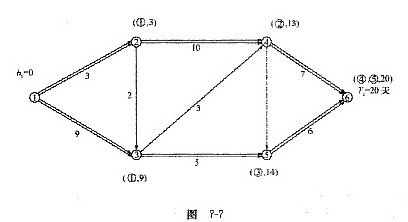
4)第四次压缩:
从图7—7可知,由于工作5—6不能再压缩,故有以下6种压缩方案:①同时压缩工作1—2和工作1—3,组合直接费用率为1.O千元/天。②同时压缩工作1—2和工作3—5,组合直接费用率为1.2千元/天。③同时压缩工作2—4和工作1—3,组合直接费用率为1.1千元/天。④同时压缩工作2—4和工作3—5,组合直接费用率为1.3千元/天。⑤同时压缩工作4—6和工作1—3,组合直接费用率为1.3千元/天。⑥同时压缩工作4—6和工作3—5,组合直接费用率为1.5千元/天。上述6种压缩方案的组合直接费用率均大于间接费用率0.8千元/天,说明继续压缩会使工程总费用增加,因此优化方案已得到,优化后的网络计划图如图7-8所示。图由箭线上方括号中数字为工作的直接费。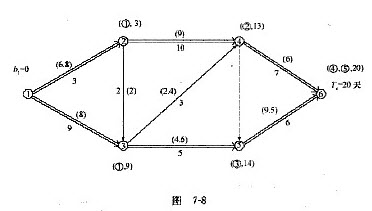
(5)优化后的工程总费用:
1)直接费总和:Cd0=(6.8+9+8+2+2.4+4.6+9.5+6)千元=48.3千元
2)间接费总和:Ci0=0.8×20千元=16千元
3)工程总费用:Ct0=Cd0+Ci0=(48.3+16.0)千元=64.3千元
(6)最低工程费用时的工期天数为20天。
