问题
问答题
已知λ=2是矩阵
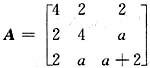的二重特征值，求a的值，并求正交矩阵Q使Q-1AQ为对角矩阵。
答案
参考答案：A是实对称矩阵，λ=2是二重根，故λ=2必有两个线性无关的特征向量，于是秩r(2E-A)=1，可得a=2。
此时[*]，于是2+2+λ3=4+4+4，知λ3=8
解(2E-A)x=0，得特征向量[*]
解(8E-A)x=0，得特征向量[*]
先将α1，α2正交化：
[*]
再将β1，β2，β3单位化，得正交矩阵：
[*]
且有[*]