问题
解答题
设数列{an}满足a1=a,an+1-1=can-c(n∈N*),其中a,c为实数,且c≠0,
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设a=0,bn=n(1-an)(n∈N*),求数列{bn}的前n项和Sn。
答案
解:(Ⅰ)∵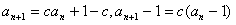 ,
,
∴当a1=a≠1时,{an-1}是首项为a-1,公比为c的等比数列,
∴ ,即
,即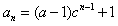 ,
,
当a=1时,an=1仍满足上式,
∴数列{an}的通项公式为 。
。
(Ⅱ)由(Ⅰ),得当a=0时,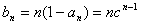 ,
,
当c=1时,bn=n,
∴Sn=b1+b2+…+bn=1+2+3+…+n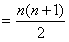 ;
;
当c≠1时,
∴Sn=b1+b2+…+bn=1+2×c+3×c2+...+n×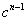 ,①
,①
由c×①,得cSn=c+2c2+3c3+…+ncn, ②
由①②两式作差,得(1-c)Sn=1+c+c2+…+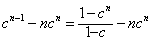 ,
,
∴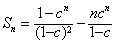 。
。
