问题
解答题
(2014·郑州模拟)已知函数f(x)=ex+ax,g(x)=ax-lnx,其中a≤0.
(1)求f(x)的极值.
(2)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.
答案
(1)f(x)的极小值为f(ln(-a))=-a+aln(-a);没有极大值
(2)(-∞,-1)
(1)f(x)的定义域为R,且f′(x)=ex+a.
当a=0时,f(x)=ex,故f(x)在R上单调递增.
从而f(x)没有极大值,也没有极小值.
当a<0时,令f′(x)=0,得x=ln(-a).
f(x)和f′(x)的情况如下:
| x | (-∞,ln(-a)) | ln(-a) | (ln(-a),+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↘ | ↗ |
故f(x)的单调递减区间为(-∞,ln(-a));
单调递增区间为(ln(-a),+∞).
从而f(x)的极小值为f(ln(-a))=-a+aln(-a);没有极大值.
(2)g(x)的定义域为(0,+∞),且g′(x)=a- =
=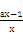 .
.
当a=0时,f(x)在R上单调递增,
g(x)在(0,+∞)上单调递减,不合题意.
当a<0时,g′(x)<0,g(x)在(0,+∞)上单调递减.
当-1≤a<0时,ln(-a)≤0,
此时f(x)在(ln(-a),+∞)上单调递增,
由于g(x)在(0,+∞)上单调递减,不合题意.
当a<-1时,ln(-a)>0,
此时f(x)在(-∞,ln(-a))上单调递减,
由于g(x)在(0,+∞)上单调递减,符合题意.
综上,a的取值范围是(-∞,-1).
