问题
问答题
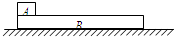
如图所示,质量为m的小木块A,放在质量为M的木板B的左端,B在水平拉力的作用下眼水平地面匀速向右运动,且A、B相对静止.某时刻撤去水平拉力,经过一段时间,B在地面上滑行了一段距离s,A在B上相对于B向右滑行了一段距离L后,A和B都停下.已知木板足够长,A、B间的动摩擦因数为μ1,B与地面间的动摩擦因数为μ2,且μ1<μ2,求撤去水平拉力后:
(1)小木块和木板各自的加速度;
(2)小木块和木板滑行时间之比;
(3)木板B移动距离s的表达式.
答案
(1)根据牛顿第二定律得,aA=μ1g
aB=μ2(M+m)g-μ1mg M
(2)因为A、B的初速度相等,末速度为零,根据v=at知,时间之比等于加速度之反比.
=t1 t2 μ2(M+m)g-μ1mg μ1Mg
(3)对A应用动能定理-f1(L+s)=0-
mv21 2
对B应用动能定理 μ1mgs-μ2(m+M)gs=0-
Mv21 2
解得:消去v解得s=
.μ1ML (μ2-μ1)(M+m)
答:(1)小木块和木板各自的加速度分别为aA=μ1g,aB=
.μ2(M+m)g-μ1mg M
(2)小木块和木板滑行时间之比
=t1 t2
.μ2(M+m)g-μ1mg μ1Mg
(3)木板B移动距离s的表达式s=
.μ1ML (μ2-μ1)(M+m)