问题
解答题
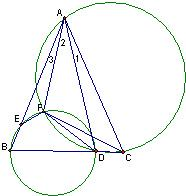
设点D为等腰△ABC的底边BC上一点,F为过A、D、C三点的圆在△ABC内的弧上一点,过B、D、F三点的圆与边AB交于点E.求证:CD•EF+DF•AE=BD•AF.
答案
证明:设AF的延长线交⊙BDF于K,
∵∠AEF=∠AKB,
∴△AEF~△AKB,因此
=EF AF
,BK AB
=AE AF
.AK AB
于是要证CD•EF+DF•AE=BD•AF(1),只需证明:CD•BK+DF•AK=BD•AB(2)
又注意到∠KBD=∠KFD=∠C.
我们有S△DCK=
CD•BK•sin∠C1 2
进一步有S△ABD=
BD•AB•sin∠C1 2 S△ADK=
AK•DF•sin∠C1 2
因此要证(2),只需证明S△ABD=S△DCK+S△ADK(3)
而(3)⇔S△ABC=S△AKC⇔BK∥AC(4)
事实上由∠BKA=∠FDB=∠KAC知(4)成立,得证.