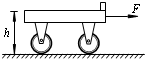
如图所示,一辆平板小车静止在水平地面上,小车的右端放置一物块(可视为质点).已知小车的质量M=4.0kg,长度l=1.0m,其上表面离地面的高度h=0.80m.物块的质量m=1.0kg,它与小车平板间的动摩擦因数μ=0.20,最大静摩擦力可以认为等于滑动摩擦力.若用水平向右的恒定拉力F=18N拉小车,经过一段时间后,物块从小车左端滑出,在物块滑出瞬间撤掉拉力F,不计小车与地面间的摩擦. 取g=10m/s2,求:
(1)拉动小车过程中拉力F所做的功;
(2)物块落地时的动能;
(3)物块落地时,物块与小车左端的水平距离.
(1)设物块运动的加速度为a1,小车运动的加速度为a2,物块从开始滑动到从小车左端滑出的时间为t.
物块所受摩擦力f=μmg,
根据牛顿第二定律f=ma1,物块的位移x1=
a1t21 2
小车所受摩擦力f′=f=μmg,
根据牛顿第二定律F-f′=Ma2,小车的位移x2=
a2t21 2
解得物块运动的加速度为a1=2 m/s2,
小车运动的加速度a2=4m/s2
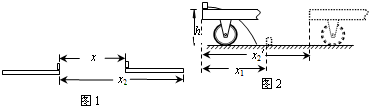
由如图1所示的几何关系可知 x2-x1=l
解得滑块在t=1s末从小车左端滑出,
小车的位移x2=
a2t2=2m,1 2
拉力F所做的功W=F x2=36J
(2)此时物块的速度大小v1=a1t=2m/s
物块滑出后做平抛运动,
机械能守恒,
m v12+mgh=E 1′1 2
物块落地时的动能为E 1′=10J
(3)物块与小车分离时,小车速度为 v2=a2t=4 m/s
物块与小车分离后向右做平抛运动,
设物块做平抛运动的时间为t′,
则t′=
=0.40 s2h g
物块做平抛运动的过程中
物块向右的水平位移 x1′=v1 t′=0.8m
小车向右的位移x2′=v2 t′=1.6m
由图2所示的几何关系可知,当物块落地时,
物块与小车在水平方向上相距x2′-x1′=0.8 m
答:(1)拉动小车过程中拉力F所做的功为36J;
(2)物块落地时的动能10J;
(3)物块落地时,物块与小车左端的水平距离为0.8 m.
