参考答案：[证法一] 因为A是正定阵，故存在正交矩阵Q，使

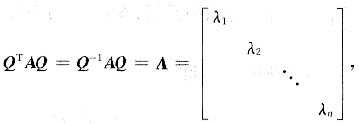
其中λ_i＞0(i=1，2，…n)，λ_i是A的特征值．
因此Q^T(A+E)Q=Q^TAQ+Q^TQ=A+E．
两端取行列式得
|A+E|=|Q^T||A+E||Q|=|Q^T(A+E)Q|=|A+E|=Ⅱ(λ_i+1)．
从而|A+E|＞1．
[证法二] 设A的n个特征值是λ₁，λ₂，…λ_n，由于A是正定矩阵，故特征值全大于0．因为A+E的特征值是λ₁+1，λ₂+1，…，λ_n+1，它们全大于1，根据|A|=Ⅱλ_i，知
|A+E|=Ⅱ(λ_i+1)＞1．

解析：[考点提示] 正定矩阵的相关计算．