问题
问答题
设非负单减函数f(x)在[0，b]上连续，0
答案
参考答案：[证] 令[*]，则
[*]
由于f(x)为非负单减函数，所以(b-x)[f(x)-f(ξ)]+2xf(x)＞0，即F’(x)＞0，故F(x)在[0，b]上单增，又因为F(0)=0，所以F(a)＞F(b)=0，即[*]．
搜题请搜索小程序“爱下问搜题”
设非负单减函数f(x)在[0，b]上连续，0
参考答案：[证] 令[*]，则
[*]
由于f(x)为非负单减函数，所以(b-x)[f(x)-f(ξ)]+2xf(x)＞0，即F’(x)＞0，故F(x)在[0，b]上单增，又因为F(0)=0，所以F(a)＞F(b)=0，即[*]．
如图是测定铝粉（含镁粉）的纯度的实验装置。所用的NaOH（足量）的物质的量浓度为4.5 mol·L－1。不同时间电子天平的读数如下表所示：
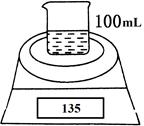
| 实验操作 | 时间/min | 电子天平的读数/g |
| 烧杯＋NaOH溶液 | 0 | 120 |
| 烧杯＋NaOH溶液＋样品 | 0 | 135 |
| 1 | 134.5 | |
| 2 | 134.1 | |
| 3 | 133.8 | |
| 4 | 133.8 |
（1）反应中生成气体的质量 g。
（2）试计算样品中铝的质量分数。(写出解题过程)
（3）反应后溶液(溶液的体积变化忽略)的c(OH－)。(写出解题过程)