问题
解答题
(选作题)
已知圆方程为y2-6ysinθ+x2-8xcosθ+7cos2θ+8=0,
(1)求圆心轨迹的参数方程C;
(2)点P(x,y)是(1)中曲线C上的动点,求2x+y的取值范围。
答案
解:(1)将圆的方程整理得:(x-4cosθ)2+(y-3sinθ)2=1,
设圆心坐标为P(x,y),
则 ;
;
(2)2x+y=8cosθ+3sinθ=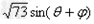 ,
,
∴ - ≤2x+y≤
≤2x+y≤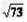 。
。
(选作题)
已知圆方程为y2-6ysinθ+x2-8xcosθ+7cos2θ+8=0,
(1)求圆心轨迹的参数方程C;
(2)点P(x,y)是(1)中曲线C上的动点,求2x+y的取值范围。
解:(1)将圆的方程整理得:(x-4cosθ)2+(y-3sinθ)2=1,
设圆心坐标为P(x,y),
则 ;
;
(2)2x+y=8cosθ+3sinθ=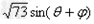 ,
,
∴ - ≤2x+y≤
≤2x+y≤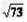 。
。