问题
问答题
设A是二阶矩阵，α为非零向量，但不是A的特征向量，且满足A2α+Aα-2α=0．
α，Aα线性无关；
答案
参考答案：设存在k1，k2，使得k1α+k2Aα=0．
若
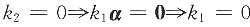(因为α≠0)，
若走
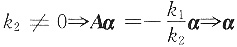是A的特征向量，矛盾．
综上，可得k1=k2=0，所以α，Aα线性无关．
搜题请搜索小程序“爱下问搜题”
设A是二阶矩阵，α为非零向量，但不是A的特征向量，且满足A2α+Aα-2α=0．
α，Aα线性无关；
参考答案：设存在k1，k2，使得k1α+k2Aα=0．
若
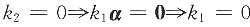(因为α≠0)，
若走
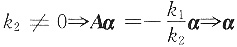是A的特征向量，矛盾．
综上，可得k1=k2=0，所以α，Aα线性无关．