阅读理解。
If you're into sports, you've seen it happen. You've probably even experienced it: basketball players
shaking hands after four quarters of knocking each other around, tennis players leaping over the net to
shake hands with their opponents (对手) after a hard-fought match, soccer players exchanging sport
shirts after an intense 90 minutes, even boxers touching gloves at the beginning of each round, then
hugging each other after beating each other into a pulp for 12 rounds. It seems like competitors in every
event, from spelling bees to hockey, behave this way. What's going on?
It's all part of sportsmanship, a great tradition in sports and competition that means playing clean and
handling both victory and defeat with grace, style, and dignity.
What is sportsmanship? Sportsmanship is defined as: playing fair, following the rules of the game,
respecting the judgment of referees and officials, treating opponents with respect.
Some people define good sportsmanship as the "golden rule" of sports-in other words, treating the
people you play with and against as you'd like to be treated yourself. You demonstrate good sportsmanship
when you show respect for yourself, your teammates, and your opponents, for the coaches on both sides,
and for the referees, judges, and other officials.
But sportsmanship isn't just reserved for the people on the field. Cheerleaders and fans also need to be
aware of how they behave during competition. Sportsmanship is a style and an attitude; and it can have a
positive influence on everyone around you.
Learning good sportsmanship means finding that the positive attitude learned on the field carries over
into other areas of life. At school, for example, you're able to appreciate the contributions made by
classmates and know how to work as part of a team to complete a project. You may enjoy more success
at work as well, because a big part of learning good sportsmanship is learning to be respectful of others,
including customers and co-workers.
1. The author introduces the topic of the passage by_____.
A. showing an interesting discussion
B. comparing several sport events
C. explaining some game rules
D. giving some specific examples
2. When players play clean, ______.
A. they play in fresh air
B. they play in a skilled way
C. they play within the rules
D. they play without hurting each other
3. The purpose of writing this passage is to ______.
A. advise readers to take some exercise
B. provide some basic sport knowledge
C. show the meaning of sportsmanship
D. expect players to compete actively
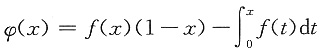 ,则
,则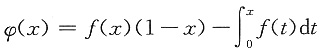 ,则
,则