问题
问答题
设f(u)为奇函数,且具有一阶连续导数,S是由锥面
 ,两球面x2+y2+z2=1与x2+y2+z2=2(z>0)所围立体的全表面,向外.求
,两球面x2+y2+z2=1与x2+y2+z2=2(z>0)所围立体的全表面,向外.求
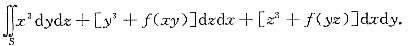
答案
参考答案:由条件知,可以用高斯公式,记S所包围的有界区域为Ω,于是
[*]
因为f是变元的奇函数,所以f’(xy)是x的偶函数,xf’(xy)是x的奇函数,所以
[*]
同理
[*]
从而
[*]
设f(u)为奇函数,且具有一阶连续导数,S是由锥面
 ,两球面x2+y2+z2=1与x2+y2+z2=2(z>0)所围立体的全表面,向外.求
,两球面x2+y2+z2=1与x2+y2+z2=2(z>0)所围立体的全表面,向外.求
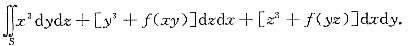
参考答案:由条件知,可以用高斯公式,记S所包围的有界区域为Ω,于是
[*]
因为f是变元的奇函数,所以f’(xy)是x的偶函数,xf’(xy)是x的奇函数,所以
[*]
同理
[*]
从而
[*]