问题
填空题
设A是三阶实对称矩阵，λ=5是A的二重特征值．对应的特征向量为ξ1=[1，-1，2]，ξ2=[1，2，1]T，则二次型f(x1，x2，x3)=XTAX在X0=[1，5，0]T的值f(1，5，0)=
=______．
答案
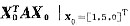参考答案：130
解析：
[分析]： 已知Aξ1=5ξ1，Aξ2=5ξ2，故二次型f(x1，x2，x3)=XTAX在特征向量处的值为
[*]
为求二次型在X0处的值，可将X0用ξ1，ξ2线性表出，设X0=x1ξ1+x2ξ2，得方程组
[*]
解得x1=-1，x2=2，即X0=-ξ1+2ξ2．
[*]