如图所示,一质量M=2.0kg的长木板静止放在光滑水平面上,在木板的右端放一质量m=1.0kg可看作质点的小物块,小物块与木板间的动摩擦因数为μ=0.2.用恒力F向右拉动木板使木板在水平面上做匀加速直线运动,经过t=1.0s后撤去该恒力,此时小物块恰好运动到距木板右端l=1.0m处.在此后的运动中小物块没有从木板上掉下来.求:
(1)小物块在加速过程中受到的摩擦力的大小和方向;
(2)作用于木板的恒力F的大小;
(3)木板的长度至少是多少?

(1)设小物块受到的摩擦力为f=μN1=μmg=0.2×1.0×10N=2N 方向水平向右.
(2)设小物块的加速度为a1,木板在恒力F作用下做匀加速直线运动时的加速度为a2,此过程中小物块的位移为s1,木板的位移为s2则
由牛顿定律及运动规律可知:f=ma1 a1=2.0m/s2
s1=
a1t2 1 2
s2=
a2t2 1 2
s2-s1=l
带入数据解得:a2=4m/s2
设木板受到的摩擦力为f’,f’=f,对木板根据牛顿第二定律:F-f’=Ma2,
则F=f’+ma2,代入数值得出F=10N.
(3)设撤去F时小物块和木板的速度分别为v1和v2,撤去F后,木板与小物块组成的系统动量守恒,
当小物块与木板相对静止时,它们具有共同速度v,
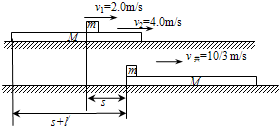
v1=a1t=2.0m/s v2=a2t=4.0m/s
根据动量守恒定律得:mv1+Mv2=(m+M)v
v=
m/s=1.0×2+2.0×4.0 1.0+2.0
m/s10 3
对小物块:根据动能定理:fs=
mv2-1 2
mv121 2
对木板:根据动能定理:-f(s+l′)=
Mv2-1 2
Mv221 2
代入数据:l′=
m 2 3
所以木板的长度至少为L=l+l′=
m≈1.7m 5 3
答:(1)小物块在加速过程中受到的摩擦力的大小为2N,方向水平向右;(2)作用于木板的恒力F的大小为10N;(3)木板的长度至少是1.7m.
