参考答案：

令f(x)=(x²-1)lnx-(x-1)²易看出f(1)=0，且有

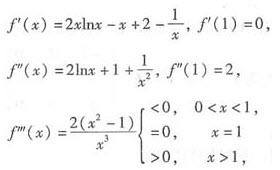
由此得x=1是f"(x)的最小点，因而f"(x)＞f"(1)=2＞0(x＞0，x≠1)；由此，f’(x)在x＞0单调增，又由f’(x)=0，f’(x)在x=1处由负变正，x=1是f(x)的最小点，故f(x)≥f(0)=0(x＞0)，所以当x＞0时，(x²-1)lnx≥(x-1)²．

解析：

[考点] 函数单调性以及函数极值点