问题
单项选择题
设f(x)在x=0处满足f’(0)=f"(0)=…=f(n)(0)=0，f(n+1)(0)＞0，则（）。
A．当n为偶数时，x=0是f(x)的极大值点
B．当n为偶数时，x=0是f(x)的极小值点
C．当n为奇数时，x=0是f(x)的极大值点
D．当n为奇数时，x=0是f(x)的极小值点
答案
参考答案：D
解析：
[考点] 函数奇偶性、极值点
因为
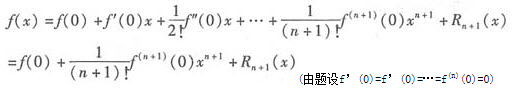
所以当|x|很小时，f(x)-f(0)与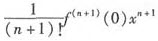
同号，而f(n+1)(0)＞0，
当n为偶数时，在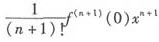
x=0点两侧异号，f(0)不是极值点；
当n为奇数时，在x=0两侧均有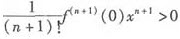
，即f(x)＞f(0)，亦即x=0为f(x)的极小值点，因此选(D)．
