问题
单项选择题
设随机变量X1，…，Xn，…相互独立，记Yn=X2n-X2n-1(n≥1)，概括大数定律，当n→∞时，
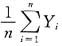依概率收敛到零，只要Xn，n≥1满足
A．数学期望存在．
B．有相同的数学期望与方差．
C．服从同一离散型分布．
D．服从同一连续型分布．
答案
参考答案：B
解析： 由题设，我们应该考虑应用大数定律来确定正确选项．由于Xn相互独立，所以Yn相互独立，选项A“缺少同分布”条件，选C、D“缺少数学期望存在”的条件，因此都不满足辛钦大数定律．所以选择B．事实上，若EXn=μ，DXn=σ1存在，则
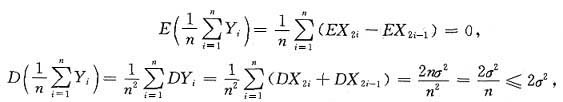
根据切比雪夫大数定律得：
．即
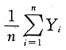依概率收敛到零．