问题
解答题
定义[p，q]为一次函数y=px+q的特征数。
（1）若特征数是[2，k-2]的一次函数为正比例函数，求k的值；
（2）设点A、B分别为抛物线y=（x+m）（x-2）与x轴、y轴的交点，其中m>0，且△OAB的面积为4，0为坐标原点，求图象过A、B两点的一次函数的特征数。
答案
解：（1）特征数为[2，k-2]的一次函数为y=2x+k -2，
∴k-2=0，
∴k=2；
（2）抛物线与x轴的交点为A1（-m，0），A2（2，0），与y轴的交点为B（0，-2m），
若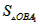
=4，则
×m×2m =4
∴m1=2，m2=-2（舍）；
若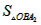
=4，则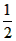
×2×2m =4
∴m=2
综上，m=2，
∴抛物线为y=（x+2）（x-2），它与x轴的交点为（-2，0）、（2，0），与y轴 的交点为（0，-4），
∴所求一次函数为y=-2x-4或y=2x-4，
∴特征数为[ -2，-4]或[2，-4]。