问题
单项选择题
假设随机变量X与Y相互独立具有非零的方差，DX≠DY，则
A．3X+1与4Y-2相关．
B．X+Y与X-Y不相关．
C．X+Y与2Y+1相互独立．
D．eX与2Y+1相互独立．
答案
参考答案：D
解析： 由于X与Y相互独立，故eX与2Y+1相互独立，选择D．
事实上，当x＞0时，P{eX≤x，2Y+1≤y}=
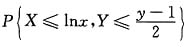
=P{X≤lnx}·
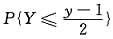=P{eX≤x)·P{2Y+1≤y}．
而当x≤0时，P{eX≤x}=0，所以P{eX≤x，2Y+1≤y}=0=P{eX≤x}·P{2Y+1≤y}，由此可知eX与2Y+1相互独立．
选项A、B、C不成立，是由于cov(3X+1，4Y-2)=12cov(X，Y)=0
3X+1与4Y-2不相关；cov(X+Y，X-Y)=cov(X，X)-cov(Y，Y)=DX=DY≠0
X+Y与X-Y相关；cov(X+Y，2Y+1)=2cov(X，Y)+2cov(Y，Y)=2DY≠0
X+Y与2Y+1相关
X+Y与2Y+1不相互独立．
