问题
单项选择题
已知随机变量X服从标准正态分布，Y=2X2+X+3，则X与Y
A．不相关且相互独立．
B．不相关且相互不独立．
C．相关且相互独立．
D．相关且相互不独立．
答案
参考答案：D
解析： 通过计算cov(X，Y)来判定．
由于X～N(0，1)，所以EX=0，DX=EX2=1，EX3=0，EXY=EX(2X2+X+3)=2EX3+EX2+3EX=1，cov(X，Y)=EXY-EXEY=1≠0
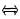X与Y相关
X与Y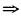不独立，选择D．
(1)理解随机变量的独立性与相关性的概念，掌握它们之间的关系及其判别方法十分重要．我们知道：两个随机变量相互独立一定不相关，反之不然．由此可知相关必不独立，既相关又相互独立的两个随机变量不存在，而不相关又不相互独立的两个随机变量是存在的．如果(X，Y)服从二维正态分布，则X与Y独立
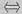X与Y不相关．
(2)如果将题目中的Y改为Y=X2，则EXY=EX3=0=EXEY，故X与Y不相关．
由于
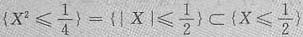，所以
，
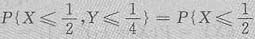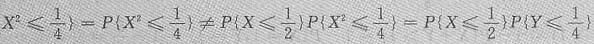故X与Y=X2不独立，此时应选择B．