参考答案：C

解析： 由于(X，Y)服从二维正态分布，故X～N(μ，σ²)，Y～N(μ，σ²)即X与Y有相同的分布，但是ρ≠0，所以X与Y不独立，选择C．
[说明] 本题可以有下面的变式：
(1)已知(X，Y)服从二维正态分布，EX=EY=μ，DX=DY=σ²，X与Y的相关系数ρ≠0，则X+Y与X-Y
(A)不相关且有相同的分布． (B)不相关且有不同的分布．
(C)相关且有相同的分布． (D)相关且有不同的分布．
答案B
由题设知
cov(X，Y)=0，DX=DY＞0，
故
cov(2X+Y，2Y+1)=4cov(X，Y)+2cov(X，1)+2cov(Y，Y)+cov(Y，1)=2DY＞0，所以2X+Y与2Y+1相关，从而断言2X+Y与2Y+1不独立，选择B．
(1)本题可以改为：2X+Y与2Y+1的相关系数ρ=______．
由于cov(X，Y)=0，DX=DY＞0，故cov(2X+Y，2Y+1)=2DY，

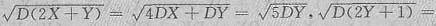
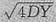，所以

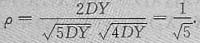
(2)若将已知条件改为：X与Y独立且有相同的分布P{X=i}=P(Y=i}=

，i=1，2，则X+Y与X-Y不相关且相互不独立．这是因为cov(X+Y，X-Y)=0，P(X+Y=2，X-Y=0}≠P{X+Y=2}P{X-Y=0}．