问题
单项选择题
设随机变量X～B(1，
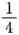)，Y～B(1，
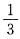)，已知PXY=1=
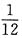，记ρ为X和Y的相关系数，则
A．ρ=1．
B．ρ=-1．
C．ρ=0，但X，Y不独立．
D．X，Y相互独立．
答案
参考答案：D
解析： cov(X，Y)=E(XY)-EX·EY=
，
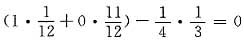所以ρ=0，A、B不成立．
P{X=1，Y=1}=P{XY=1}=
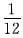=P{X=1}P{Y=1}；
P{X=0，Y=1}=P{Y=1}-P{X=1，Y=1}
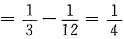=P{X=0}P{Y=1}；
同理可以证明P{X=1，Y=0}=P{X=1}P{Y=0}
P{X=0，Y=0}=P{X=0}P{Y=0}
总之X，Y相互独立．
对X～B(1，p1)，Y～B(1，p2)的两随机变量的独立性
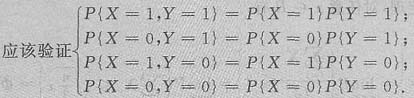
但实际上只要验证以上四个等式中一个成立，其他三个条件就一定成立．
例如P{X=1，Y=1}=P{X=1}P{Y=1}成立，
P{X=0，Y=1}=P{Y=1}-P{X=1，Y=1}=P{Y=1}-P{X=1}P{Y=1}
=P(Y=1}[1-P{X=1}]=P{X=0}P{Y=1}．
P{X=0，Y=0}=P{X=0}-P{X=0，Y=1}=P{X=0}-P{X=0}P{Y=1}
=P{X=0}[1-P{Y=1}]=P{X=0}P{Y=0}．