问题
单项选择题
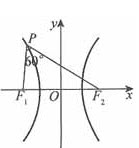
如图，双曲线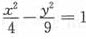
的左、右焦点分别记为F1，F2，双曲线上的点P使得∠F1PF2=60°，则△PF1F2的面积=（）。
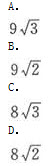
A.A
B.B
C.C
D.D
答案
参考答案：A
解析：
根据双曲线的定义可知，|PF1-PF2|=2a=4，F1F2=2c=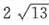
。
在焦点三角形△F1PF2中，由余弦定理可知，
=|PF1-PF2|2+2PF1·PF2-2PF1·PF2cos∠F1PF2
=|PF1-PF2|2+2PF1·PF2(1-cos∠F1PF2)
即
，从而PF1·PF2=36
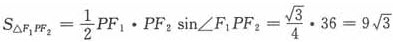，所以正确答案为A。
当然也可以直接采用双曲线焦点三角形面积公式来求解，即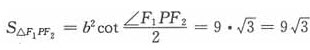
。