问题
单项选择题
设P是双曲线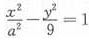
上一点，双曲线的一条渐近线方程为3x-2y=0，F1、F2分别是双曲线的左、右焦点。若|PF1|=3，则|PF2|=（）。
A．1或5
B．6
C．7
D．9
答案
参考答案：C
解析：
由双曲线方程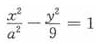
，得b=3，
因为渐近线方程为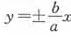
，已知渐近线方程为3x-2y=0，即
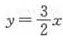，所以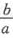
=
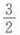，得a=2，
由双曲线定义||PF1|-|PF2||=2a，
因为|PF1|=3，故|PF2|=7或|PF2|=-1(舍)，
故|PF2|=7，
故正确答案为C。