问题
问答题
设函数f(x)与g(x)都可导,且F(x)=g(x)|f(x)|,求证:
(Ⅰ) 当f(x0)≠0时,F(x)在点x=x0处必可导;
(Ⅱ) 当f(x0)=0时,F(x)在点x=x0处可导的充分必要条件是f’(x0)g(x0)=0.
答案
参考答案:[证明] (Ⅰ) 当f(x0)≠0时,由f(x)的连续性知:存在δ>0,使得当|x-x0|<δ时f(x)与f(x0)同号.若f(x0)>0,则当|x-x0|<δ时有
F(x)=g(x)|f(x)|=g(x)f(x),
从而F(x)在x=x0处可导,且F’(x0)=g(x0)f’(x0)+g’(xo)f(x0).类似可证当f(x0)<0时F(x)也在x=x0处可导.
(Ⅱ) 当f(x0)=0时,F(x0)=g(x0)|f(x0)|=0,从而F(x)在点x=x0处的左导数与右导数分别是
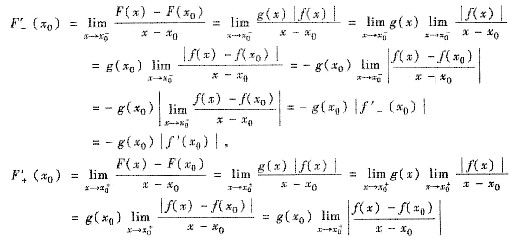

故当f(x0)=0时,|F(x)|在点x=x0处可导的充分必要条件为
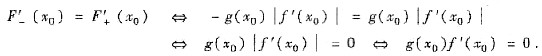
此外,不难发现,此时F(x)=g(x)|f(x)|在点x=x0处的导数F’(x0)=0.
解析:
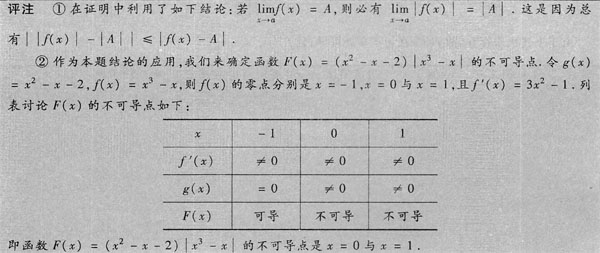

 部分冠折断,已作根管治疗。
部分冠折断,已作根管治疗。