阅读理解。
垂钓
①去年夏天我与妻子买票参加了一个民间旅行团,从牡丹江出发,到俄罗斯的海参崴游玩。海参崴的主要魅力在于海,我们下榻的旅馆面对海,每天除了在阳台上看海,还要一次次下到海岸的最外沿,静静地看。海参崴的海与别处不同,深灰色的迷雾中透露出巨大的恐怖。我们眯缝着眼睛,把脖子缩进衣领,立即成了大自然凛冽威仪下的可怜虫。其实岂止我们,连海鸥也只在岸边盘旋,不敢远翔,四五条猎犬在沙滩上对着海浪狂叫,但才吠几声又缩脚逃回。逃回后又回头吠叫,呜呜的风声中永远夹带着这种凄惶的吠叫声,直到深更半夜。
②在一个小小的弯角上,我们发现,端坐着一胖一瘦两个垂钓的老人。
③胖老人听见脚步声朝我们眨眼算是打了招呼,他回身举起钓竿把他的成果朝我们扬了一扬,原来他的钓绳上挂了六个小小的钓钩,每个钓钩上都是一条小鱼。他把六条小鱼摘下来放进身边的水桶里,然后再次下钩,半分钟不到他又起钩,又是六条挂在上面。就这样,他忙忙碌碌地下钩起钩,我妻子走近前去一看,水桶里已有半桶小鱼。
④奇怪的是,只离他两米远的瘦老人却纹丝不动。为什么一条鱼也不上他的钩呢?正纳闷,水波轻轻一动,他缓缓起竿,没有鱼,但一看钓钩却硕大无比,原来他只想钓大鱼。在他眼中,胖老人忙忙碌碌地钓起那一大堆鱼,根本是在糟蹋钓鱼者的取舍标准和堂皇形象。伟大的钓鱼者是安坐着与大海进行谈判的人类代表,而不是在等待对方琐碎的施舍。
⑤胖老人每次起竿都要用眼角瞟一下瘦老人,好像在说:“你就这么熬下去吧,伟大的谈判者!”而瘦老人只以泥塑木雕般的安静来回答。两个都在嘲讽对方,两个谁也不服谁。
⑥过了不久,胖老人起身,提起满满的鱼桶走了,快乐地朝我们扮了一个鬼脸,却连笑声也没有发出,脚步如胜利者凯旋。瘦老人仍在端坐着,夕阳照着他倔强的身躯,他用背影来鄙视同伴的浅薄。暮色苍茫了,我们必须回去,走了一段路回身,看到瘦小的身影还在与大海对峙。此时的海,已经更加狰狞昏暗。狗声越来越响,夜开始了。
⑦妻子说:“我已经明白,为什么一个这么胖,一个这么瘦了。一个更加物质,一个更加精神,人世间的精神总是固执而瘦削的,对么?”
⑧我说:“说得好。但也可以说,一个是喜剧美,一个是悲剧美。他们天天在互相批判,但加在一起才是完整的人类。”
⑨确实,他们谁也离不开谁。没有瘦老人,胖老人的丰收何以证明?没有胖老人,瘦老人的固守有何意义?大海中多的是鱼,谁的丰收都不足挂齿;大海有漫长的历史,谁的固守都是一瞬间。因此,他们的价值都得有对手来证明。可以设想,哪一天,胖老人见不到瘦老人,或瘦老人见不到胖老人,将会何等惶恐。在这个意义上,最大的对手也就是最好的朋友,很难分开。
⑩两位老人身体都很好,我想此时此刻,他们一定还坐在海边,像两座恒久的雕塑,组成我们心中的海参崴。
1.选文中的“取舍标准”和“堂皇形象”分别指什么?
_________________________________________________。
2.胖老人和瘦老人互相嘲讽对方的原因是什么?
_________________________________________________。
3.“大海中多的是鱼,谁的丰收都不足挂齿;大海有漫长的历史,谁的固守都是一瞬间。”作者说这句话的意义何在?
_________________________________________________。
4.第9段中说“最大的对手也是最好的朋友”,请说其原因?
_________________________________________________。
5.文末说两位老人“像两座恒久的雕塑”,请根据其中的含义,举出生活中一个例子并作简要说明。
_________________________________________________。
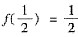 .求证:对任何满足0<k<1的常数k,存在ξ∈(0,1),使f’(ξ)=-k.
.求证:对任何满足0<k<1的常数k,存在ξ∈(0,1),使f’(ξ)=-k.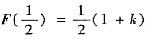 ,F(1)=1+k,即
,F(1)=1+k,即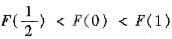 .
.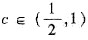 使F(c)=F(0),从而F(x)在区间[0,c]上满足罗尔定理的条件,于是,存在ξ∈(0,C)
使F(c)=F(0),从而F(x)在区间[0,c]上满足罗尔定理的条件,于是,存在ξ∈(0,C)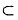 (0,1),使
(0,1),使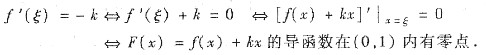
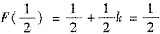 (1+k),从而
(1+k),从而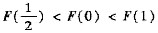 .即F(0)是
.即F(0)是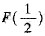 和F(1)的一个中间值,由F(x)的连续性和有界闭区间上连续函数的性质知
和F(1)的一个中间值,由F(x)的连续性和有界闭区间上连续函数的性质知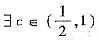 使F(c)=F(0),由此可见只需在闭区间[0,c]上对F(x)应用罗尔定理即可得出要证明的结论.
使F(c)=F(0),由此可见只需在闭区间[0,c]上对F(x)应用罗尔定理即可得出要证明的结论.
