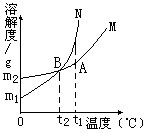
问题
解答题
已知数列{an}满足a1=1,an=an-1+3n-2(n≥2)。
(1)求a2,a3;
(2)求数列{an}的通项公式。
答案
解:(1)由已知:{an}满足a1=1,an=an-1+3n-2(n≥2),
∴a2=a1+4=5,a3=a2+7=12。
(2)由已知:an=an-1+3n-2(n≥2)得:
an-an-1=3n-2,
由递推关系,得
an-1-an-2=3n-5,…,a3-a2=7,a2-a1=4,叠加得:
an-a1=4+7+…+3n-2
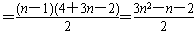
∴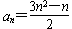 (n≥2)
(n≥2)
当n=1时,
∴数列{an}的通项公式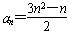 。
。