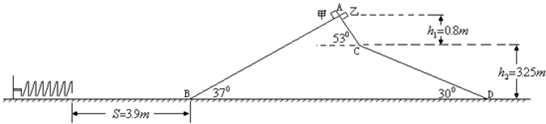
如图所示,静止在粗糙水平面上的斜面体有三个光滑斜面AB、AC和CD.已知斜面AB与水平方向成37°角,斜面AC与水平方向成53°角,斜面CD与水平方向成30°角,A点与C点的竖直高度为h1=0.8m,C点与D点的竖直高度为h2=3.25m.在B点左侧的水平面上有一个一端固定的轻质弹簧,自然长度时弹簧右端到B点的水平距离为s=3.9m.质量均为m=1kg的物体甲和乙同时从顶点A由静止释放,之后甲沿斜面AB下滑,乙沿AC下滑.在甲乙两物体下滑过程中,斜面体始终处于静止状态,且两物体运动中经过B点、C点、D点时,速度大小不改变,只改变方向.甲进入水平面后向左运动压缩弹簧的最大压缩量为x=0.1m,乙物体进入水平面后便向右运动最终停止.已知甲物体与水平面的动摩擦因数为μ=0.6,sin37°=0.6,cos37°=0.8,g取10m/s2.求:
(1)弹簧的最大弹性势能为多少?
(2)甲物体最终停止位置距B点多远?
(3)通过计算,说明甲乙两物体是否同时滑到水平面上?
(1)当滑块甲运动到最左端时,弹簧的弹性势能最大,对滑块甲从A到最左端过程运用动能定理,得到
mg(h1+h2)-μmg(S+x)-W弹=0-0
弹簧弹力做的功等于弹性势能增加量,故
Epm=W弹
解得
Epm=mg(h1+h2)-μmg(S+x)=1×10×(0.8+3.25)-0.6×1×10×(3.9+0.1)=16.5J
即弹簧的最大弹性势能为16.5J.
(2)对甲物体从开始到停止运动的整个过程运用动能定理,有
mg(h1+h2)-μmg•L=0-0
解得
L=
=6.75mh1+h2 μ
故甲物体最终停止位置距B点为:x1=2(h1+h2)-L=1.25m.
(3)甲物体受重力、支持力,根据牛顿第二定律,有
mgsin37°=ma1
根据位移时间公式,有
=h1+h2 sin37°
a11 2 t 21
解得
t1=1.5s
对于乙物体,在倾角为53°的斜面上时,加速度设为a2,在倾角为30°的斜面上时,加速度设为a3
根据牛顿第二定律,有
mgsin53°=ma2
mgsin30°=ma3
根据运动学公式,有
=h1 sin53°
a21 2 t 22
v=a2t2
=vt3+h2 sin30°
a31 2 t 23
解得
t2=0.5s
t3=1s
故t1=t2+t3
即甲乙两物体同时到达水平面上.
