问题
问答题
设总体X的概率分布为
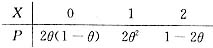 ,其中参数θ∈
,其中参数θ∈
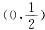 未知,以Ni表示来自总体X的简单随机样本(样本容量为n)中等于i的个数(i=0,1,2).
未知,以Ni表示来自总体X的简单随机样本(样本容量为n)中等于i的个数(i=0,1,2).
(Ⅰ)求参数θ的矩估计量
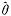 ;
;
(Ⅱ)求常数a0,a1,a2,使
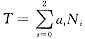 为θ2的无偏估计量,并求T的方差.
为θ2的无偏估计量,并求T的方差.
答案
参考答案:[分析与解答] (Ⅰ)参数0就一个,用
 .
.
EX=0·2θ(1-θ)+1·2θ2+2·(1-2θ)=2θ2-4θ+2=2(θ-1)2
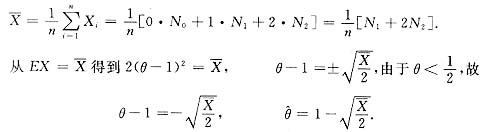
(Ⅱ)使
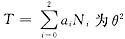 的无偏估计量,即要求ET-θ2.
的无偏估计量,即要求ET-θ2.
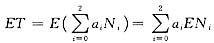 ,Ni表示来自总体X的简单随机样本中等于i的个数,(i=0,1,2).
,Ni表示来自总体X的简单随机样本中等于i的个数,(i=0,1,2).
如果把样本X1,X2,…,Xn中每个Xj取i值看成是一次试验成功,Xj不取i值看成是一次试验失败,则样本的n个分量看成是n重独立重复试验.如果取i值即试验成功的概率为p1,则Ni~B(n,pi),ENi=npi,DNi=npi(1-pi)
所以
ET=a0n2θ(1-θ)+a1n2θ2+a2n(1-2θ)=θ2
即
(2a1n-2a0n)θ2+(2a0n-2a2n)θ+a2n=θ2
因此
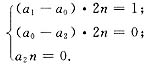 由此解得
由此解得
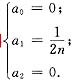
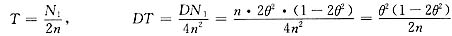 .
.
