问题
问答题
已知数列an中a1=3,a2=5,其前n项和满足Sn+Sn-2=2Sn-1+2n-1(n≥3).
(1)试求数列an的通项公式.
(2)令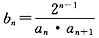 ,Tn是数列bn的前n项和,证明:
,Tn是数列bn的前n项和,证明: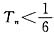 .
.
(3)证明:对任意的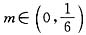 ,均存在n0∈N*,使得(2)中的Tn>m成立.
,均存在n0∈N*,使得(2)中的Tn>m成立.
答案
参考答案:
(1)解:由Sn+Sn-2=2Sn-1+2n-1(n≥3)得,Sn-Sn-1=Sn-1-Sn-2+2n-1(n≥3).
∵an=Sn-Sn-1,∴an=an-1+2n-1(n≥3),即an-an-1=2n-1(n≥3).
又∵a2-a1=5-3=2(n≥2),∴an-an-1=2n-1(n≥2).
an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2n-1+2n-2+2n-3+…+21+3=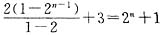 .
.
故数列{an}的通项公式为an=2n+1.
(2)证明:∵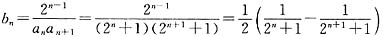 ,
,
∴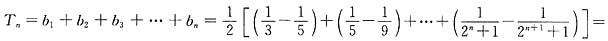
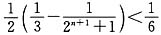 .
.
(3)证明:由(2)可知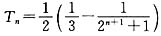 ,
,
若Tn>m,则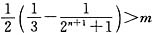 ,化简得
,化简得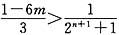 .
.
∵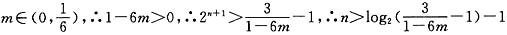 .
.
当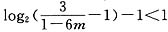 ,即
,即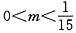 时,取n0=1即可.
时,取n0=1即可.
当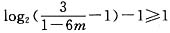 ,即
,即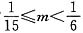 .
.
记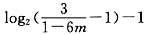 的整数部分为s,取n0=s+1即可.
的整数部分为s,取n0=s+1即可.
综上可知,对任意的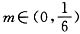 均存在n0∈N*使得(2)中的Tn>m成立.
均存在n0∈N*使得(2)中的Tn>m成立.

 k some water?
k some water?