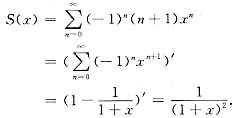问题
问答题
设
 ,(n≥0)
,(n≥0)
(Ⅰ)证明:当|x|<1时,幂级数
 收敛;
收敛;
(Ⅱ)求该幂级数的和函数S(x).
答案
参考答案:[解] (Ⅰ)由
 知
知

则幂级数
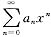 的收敛半径为R=1,故当|x|<1时,幂级数
的收敛半径为R=1,故当|x|<1时,幂级数
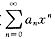 收敛,又
收敛,又
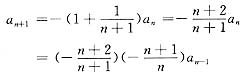
由此可知
an=(-1)n(n+1) (n≥0).
(Ⅱ)令
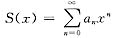 ,则
,则
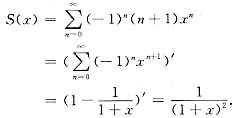
设
 ,(n≥0)
,(n≥0)
(Ⅰ)证明:当|x|<1时,幂级数
 收敛;
收敛;
(Ⅱ)求该幂级数的和函数S(x).
参考答案:[解] (Ⅰ)由
 知
知

则幂级数
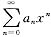 的收敛半径为R=1,故当|x|<1时,幂级数
的收敛半径为R=1,故当|x|<1时,幂级数
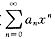 收敛,又
收敛,又
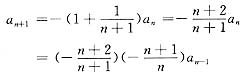
由此可知
an=(-1)n(n+1) (n≥0).
(Ⅱ)令
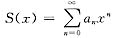 ,则
,则