问题
单项选择题
设f(x)在x=x0处取得极大值，则
(A) f′(x0)=0．
(B) 存在δ＞0，使f(x)在(x0-δ，x0)内单调增；而在(x0，x0+δ)内单调减．
(C) 存在δ＞0，在(x0-δ，x0)内f′(x0)＞0；而在(x0，x0+δ)内f′(x)＜0．
(D) -f(x)在x=x0处取极小值．
答案
参考答案：D
解析： 由极大值的定义知，存在δ＞0，当x∈(x0-δ，x0+δ)时f(x)≤f(x0)
从而有
-f(x)≥-f(x0)
由极值定义知，-f(x)在x=x0处取极小值．故应选(D)．
[评注] 其余选项都是错误的．事实上，为了方便可取x0=0，若取f(x)=-|x|，显然f(x)在x=0处取极大值，但f′(0)不存在，则(A)不正确．
若取
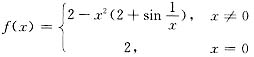
由极值定义可知f(x)在x=0处取极大值，但，当x≠0时
而
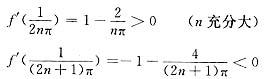
即在x=0的任何右半邻域内，始终存在导数为正的点
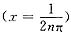和导数为负的点
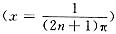，从而(B)和(C)都是错误的．
注意，本题的前三个选项都是同学们易犯的错误，应特别注意!
