问题
单项选择题
设n(≥3)维向量α1=(a,1,1,…,1)T,α2=(1,a,1,…,1)T,α3=(1,1,α,…,1)T,…,αn=(1,1,1,…,a)T.若秩r(α1,α2,α3,…,αn)=n-1,则a
(A) 1. (B) -1. (C) 1-n. (D) n-1.
答案
参考答案:C
解析: 令
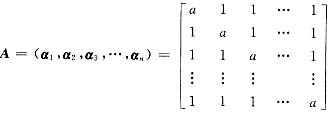
对A作初等行变换,把第1行的-1倍依次加至第2,3,…,n各行,又因r(A)=n-1,显然有a≠1.把2,3,…,n行约去1-a后再加至第1行就有

可见
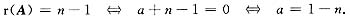
[注] 由于矩阵A是实对称矩阵,必有A~Λ.如果你能快捷地求出矩阵A的特征值,那么通过r(A)=r(Λ)=n-1可以更好地求出a.
