问题
问答题
过点C(0,1)的椭圆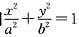 (a>b>0)的离心率为
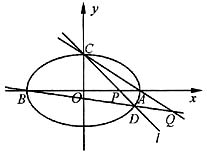
(a>b>0)的离心率为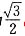 ,椭圆与x轴交于两点A(a,0)、B(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
,椭圆与x轴交于两点A(a,0)、B(-a,0),过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
(1)当直线l过椭圆右焦点时,求线段CD的长;
(2)当点P异于点B时,求证: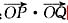 为定值.
为定值.
答案
参考答案:
(1)解:由已知得b=1,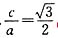 ,解得a=2,所以椭圆方程为
,解得a=2,所以椭圆方程为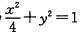 .
.
椭圆的右焦点为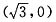 ,此时直线l的方程为
,此时直线l的方程为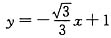 ,代入椭圆方程得7x2-
,代入椭圆方程得7x2-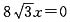 ,解得x1=0,
,解得x1=0,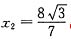 ,代入直线l的方程得y1=1,
,代入直线l的方程得y1=1,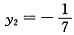 .所以,D点的坐标为
.所以,D点的坐标为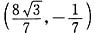 ,
,
故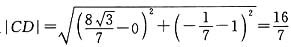 .
.
(2)证明:当直线l与x轴垂直时与题意不符.
设直线l的方程为y=kx+1(k≠0且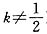 ,代入椭圆方程得(4k2+1)x2+8kx=0.解得x1=0,
,代入椭圆方程得(4k2+1)x2+8kx=0.解得x1=0, ,代入直线l的方程得
,代入直线l的方程得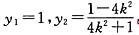 ,
,
∴D点的坐标为 .
.
又∵直线AC的方程为 ,直线BD的方程为
,直线BD的方程为 ,联立得
,联立得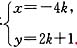 .
.
∴Q点的坐标为(-4k,2k+1),又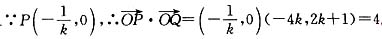 .故
.故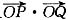 为定值.
为定值.
