阅读下列函数说明和C代码，填入 (n) 处字句，并回答相应问题。
[说明]
背包问题就是有不同价值、不同重量的物品n件，求从这n件物品中选取一部分物品的选择方案，使选中物品的总重量不超过指定的限制重量，而且选中物品的价值之和为最大。
背包问题是一个典型的NP完全难题。对该问题求解方法的研究无论是在理论上，还是在实践中都具有一定的意义。如管理中的资源分配、投资决策、装载问题等均可建模为背包问题。
常用的背包问题求解方法很多，但本题中采用了一种新的算法来求解背包问题。该算法思想为：首先要对物品进行价重比排序，然后按价重比从大到小依次装进包裹。这种方法并不能找到最佳的方案，因为有某些特殊情况存在，但只要把包中重量最大的物品取出，继续装入，直到达到limitweight，这时的物品就是limit weight的最大价值。这种算法不需要逐个进行试探，所以在数据非常大时，执行效率主要由排序的时间复杂度决定。该算法的流程图为图11-4。
仔细阅读程序说明和C程序流程图及源码，回答问题1和问题2。
[流程图11-4]

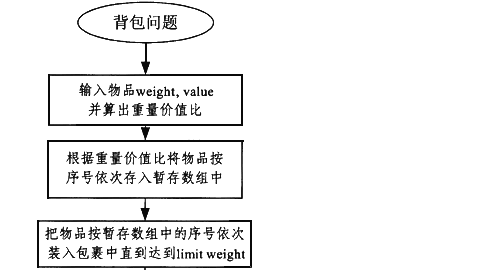
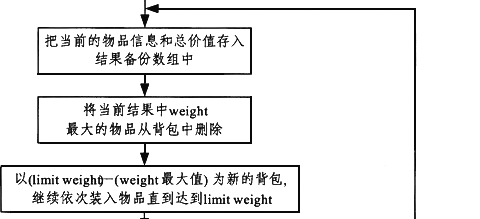
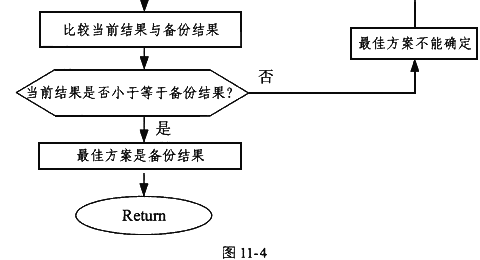
[程序说明]
struct Thing：物品结构
typedef struct Bag：背包结构类型
input ( )：将物品按序号依次存入数组函数
inbag ( )：物品按物价比入包函数
init ( )：初始化函数
sort ( )：对物品按价格重量比排序函数
outbag ( )：取出包中weiht最大的物品函数
print ( )：最佳方案输出函数
[C程序]
#define N 255
struct Thing {
double weight;
double value;
double dens;
}thing[N];
typedef stmct Bag {
Thing thing [N];
double weighttmp;
double sumvalue;
}bag,best;
inbag ( )
{
do{
bag.thing[i]=thing[i]
(1)
(2)
i++;
}while ( (3) )
}
init ( )
{
for (inti=0; i＜N; i++)
{
input (thing[i].weight, thing [i].value)
thing [i].dens=thing[i].value/thing [i].weight;
};
}
main ( )
{
init ( );
sort ( );
inbag ( );
do {
best=bag; //把包中物品放入暂存数组
outbag ( ); //取出包中weight最大的物品
(4)
}while ( (5) )
print (best)； //输出temp因为是最佳方案
}