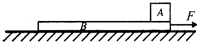
如图所示,在光滑水平地面上静放着质量mA=2kg的滑块A(可看成质点)和质量mB=4kg、长L=6m的薄板B.设A、B间动摩擦因数为μ=0.2,且A、B之间的最大静摩擦力与滑动摩擦力大小相等.因向B板施加水平拉力F=20N,F作用2s后撤去F,取g=10m/s2.求:
(1)拉力F所做的功.
(2)薄板B在水平地面上运动的最终速度.
(1)设力F作用时A、B相对静止地一起运动,
则它们的共同加速度a=
=F mA+mB
m/s2=3.3m/s220 (2+4)
而B对A最大静摩擦力使A产生的加速度aA=
=μg=0.2×10m/s2=2m/s2μmAg mA
∵aA<a,故开始时A、B间发生相对运动
对于B:根据牛顿第二运动定律有 F-μmAg=mBaB
则B的加速度aB=
=F-μmAg mB
m/s2=4m/s220-0.2×2×10 4
若B板足够长,t=2s时A、B对地位移:SA=
aAt2=1 2
×2×22m=4m1 2
SB=
aBt2=1 2
×4×22m=8m1 2
则A、B间相对位移△S=SB-SA=8m-4m=4m<L=6m
说明t=2s时,撤去外力F时A未到达B的末端,
所以拉力做的功为:W=F•SB=20×8J=160J
(2)力F撤消瞬间,滑块A的速度 υA=aAt=2×2m/s=4m/s
板B的速度 υB=aBt=4×2m/s=8m/s
在t=2s后,滑块A作初速度为υA=4m/s、aA=2m/s2的匀加速直线运动;板B作初速度为υB=8m/s、a′B=
=μmAg mB
=1m/s2的匀减速直线运动;0.2×2×10 4
判断A、B能否以共同速度运动:
t=2s时A离B的末端SAB=6m-4m=2m,设A不会从B的末端滑出,且到达末端时与A有共同速度υ,从t=2s到达共同速度期间A、B间相对位移为S则:μmAgS=
mA1 2
+υ 2A
mB1 2
-υ 2B
(mA+mB)υ21 2
根据动量守恒定律,有:mAυA+mBυB=(mA+mB)υ
代入数字解得:S=
m>2m,所以A、B不可能有共同速度,A会从B的末端滑出;8 3
求υ'B:设A滑离B时的速度为υ'A、B的速度为υ'B,
有:μmAgSAB=
mA1 2
+υ 2A
mB1 2
-(υ 2B
mAυ1 2
+′ 2A
mBυ1 2
)′ 2B
mAυA+mBυB=mAυ'A+mBυ'B
代入数据,解得υ′B=
m/s=7.33m/s或υ′B=6m/s舍去22 3
答:(1)拉力F所做的功为160J.
(2)薄板B在水平地面上运动的最终速度7.33m/s.
