问题
问答题
x2+y2的最小值为2
(1)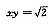 ;(2)x,y是关于t的方程t2-2at+a+2=0的两个实根.
;(2)x,y是关于t的方程t2-2at+a+2=0的两个实根.
答案
参考答案:
B
解析:
显然(1)单独不成立,对于(2),由韦达定理得: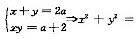 (x+y)2-2xy=4a2-2(a+2),因为方程有两个根,因此两根△=4a2-4(a+2)≥0
(x+y)2-2xy=4a2-2(a+2),因为方程有两个根,因此两根△=4a2-4(a+2)≥0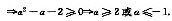
对于4a2-2(a+2)=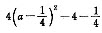 .因此当a=-1时,取到最小值.
.因此当a=-1时,取到最小值.
这样可得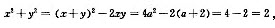 ,选择B.
,选择B.
x2+y2的最小值为2
(1)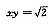 ;(2)x,y是关于t的方程t2-2at+a+2=0的两个实根.
;(2)x,y是关于t的方程t2-2at+a+2=0的两个实根.
参考答案:
B
解析:
显然(1)单独不成立,对于(2),由韦达定理得: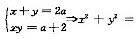 (x+y)2-2xy=4a2-2(a+2),因为方程有两个根,因此两根△=4a2-4(a+2)≥0
(x+y)2-2xy=4a2-2(a+2),因为方程有两个根,因此两根△=4a2-4(a+2)≥0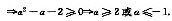
对于4a2-2(a+2)=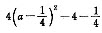 .因此当a=-1时,取到最小值.
.因此当a=-1时,取到最小值.
这样可得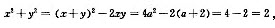 ,选择B.
,选择B.