问题
问答题
线性方程组
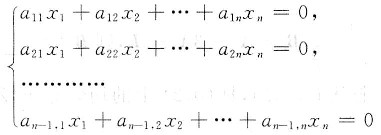
的系数矩阵为A,Mi(i=1,2,…n)是从A中划去第i列所得的n-1阶子式.证明:
(1) (M1,-M2,…,(-1)n-1Mn)是该方程组的一个解向量;
(2) 若r(A)=n-1,则方程组的解都是(M1,-M2,…,(-1)n-1Mn)的倍数.
答案
参考答案:(1) 因为Mi(i=1,2,…,n)是从A中划去第i列所得的n-1阶子式,所以它也是元素ani的余子式.
由代数余子式的性质可知,某一行元素的代数余子式与其它行对应元素之积的和为零.故A(M1,-M2,…,(-1)n-1Mn)=0.即可知(M1,-M2,…,(-1)n-1Mn)是该方程组的一个解向量.
(2) 若r(A)=n-1,则方程组的解含有1个解向量,根据(1)可知,该解向量为(M1,-M2,…,(-1)n-1Mn),则方程组的通解为x=k(M1,-M2,…,(-1)n-1Mn),其中k为任意实数.
即可得,若r(A)=n-1,则方程组的解都是(M1,-M2…,(-1)n-1Mn)的倍数.
解析:[考点提示] 线性方程组的解.
