问题
问答题
设f(x)在区间[0,1]上可微,且满足条件
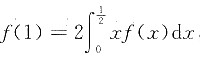 ,试证:存在ξ∈(0,1),使f(ξ)+ξf(ξ)=0.
,试证:存在ξ∈(0,1),使f(ξ)+ξf(ξ)=0.
答案
参考答案:由特证结论可知,若令ψ(x)=xf(x),则
ψ’(x)=f(x)+xf’(x).
因此,只需证明ψ(x)在[0,1]内某一区间上满足罗尔定理的条件.
令ψ(x)=xf(x),由积分中值定理可知,存在[*]使
[*]
由已知条件,有[*]
于是ψ(1)=f(1)=ψ(η),
并且ψ(x)在[η,1]上连续,在(η,1)上可导,故由罗尔定理可知,存在ξ∈(77,1)[*](0,1)使得ψ’(ξ)=0,
即f(ξ)+ξf’(ξ)=0.
解析:[考点提示] 微分中值定理的应用.
