问题
问答题
求微分方程y"+4y=3|sinx|在[-π,π]上满足条件
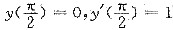 的特解,
的特解,
答案
参考答案:相应齐次方程之特征方程为
[*]
故对应齐次方程的通解为
Y=C1cos2x+C2sin2x.
设非齐次方程的特解为
y*=acosx+bsinx,
代入方程
[*]
得a=0,b=[*]1,故原方程的通解为
[*]
由初始条件[*]
在[0,π]上求得C3=1,C4=-[*],即
[*]
由此式可知,x=0时,y=1,y’=0,利用这个条件及所求解在x=0处的连续性与可导性,可定出
[*]
因此,原方程在[-π,π]上满足初始条件的解为
[*]
解析:
[分析]: 这是二阶常系数线性非齐次方程,因非齐次项含绝对值符号,故需分两种情形讨论,求出通解后,再由初始条件定出特解.
