问题
填空题
曲线
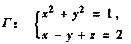 在点P
在点P
 处的切线方程是______.
处的切线方程是______.
答案
参考答案:[*]或[*]
解析:[分析一] 易写出题设[*]的参数方程
x=cost, y=sint, z=2-cost+sint.
点P在[*]上,对应[*]在P点的切向量
[*]
[*]在P点切线方程是
[*]
[分析二] 曲线[*]作为两曲面的交线,在P点的切向量
τ=grad(x2+y2-1)×grad(x-y+z-2)|P
[*]
其余同前.
[分析三] 若用交面式表示切线,由x2+y2=1在P点的法向量
[*]
求得该柱面在P点的切平面方程为[*]即[*]
[*]在P点的切线方程是[*]
