问题
问答题
设离散型二维随机变量(X,Y)的取值为(xi,yi)(i,j=1,2),且
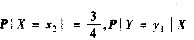
 试求:
试求:
(Ⅰ)二维随机变量(X,Y)的联合概率分布;
(Ⅱ)X与Y的相关系数ρXY;
(Ⅲ)条件概率PY=yj|X=x1,j=1,2.
答案
参考答案:
[分析]: 依题意,随机变量X与Y的可能取值分别为x1,x2与y1,y2,且
[*]
又题设[*]
于是有P{X=x1|Y=y1}=P{X=x1},
即事件{X=x1}与事件{Y=y1}相互独立,因而{X=x1}的对立事件{X=x2}与{Y=y1}独立,且{X=x1}与{Y=y1}的对立事件{Y=y2}独立;{X=x2}与{Y=y2}独立,即X与Y相互独立.
[解] (Ⅰ)因X与Y独立,所以有
[*]
或[*]
于是(X,Y)的联合概率分布为
[*]
(Ⅱ)由(Ⅰ)知X与Y独立,因此它们的相关系数ρXY=0.
(Ⅲ)因X与Y独立,所以P[{Y=yj|X=x1}=P{Y=yj
