问题
问答题
设
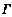:x=x(t)，y=y(t)(α≤t≤β)是区域D内的光滑曲线，即x(t)．y(t)在[α,β]有连续的导数且x’2(t)+y’2(t)≠0，
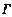的端点为A，B．f(x，y)在D内有连续的偏导数，且f(A)=f(B)．
求证：(Ⅰ)存在t0∈(α，β)，相应地有P0(x0，y0)∈，
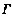,x0=x(t0)．y0=y(t0)，使得
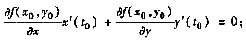
(Ⅱ)f(x，y)在点P0处沿
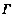的切线方向的方向导数为零．
答案
参考答案：[分析与证明] (Ⅰ)当(x，y)∈[*]时，f(x，y)变成t的一元函数f(x(t)，y(t))，记为Φ(t)．由条件知，Φ(t)在[α，β]有连续导数，不妨设A，B分别对应参数t=α，t=β，于是Φ(α)=f(A)，Φ(β)=f(B)[*]Φ(α)=Φ(β)．由罗尔定理[*]使得
Φ’(t0)=0 ①
记P0点对应的参数为t0，即P0为(x(t0)，y(t0))=(x0，y0)∈[*]
Φ(t)是二元函数f(x，y)与一元函数x=x(t)，y=y(t)的复合，由复合函数求导法得
[*]
其中x=x(t)，y=y(t)．于是，令t=t0，由①得
[*]
(Ⅱ)注意曲线[*]在点P0处的切向量是(x’(t0)，y’(t0))，单位切向量
[*]
因此，由②式得
[*]
由[*]及方向导数的计算公式得
[*]