问题
问答题
n维列向量α1，α2，…，αn-1线性无关，且与非零向量β1，β2都正交，试证：
β1，β2线性相关；
答案
参考答案：用α1，α2，…，αn-1，构造(n-1)×n矩阵：
. 由于
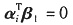(1≤i≤n-1)，从而Aβ1=0. 表明β1是齐次方程组Ax=0的非零解. 同理，β2也是AX=0的非零解. 因为r(A)=r(α1，α2，…，αn-1)=n-1，所以AX=0的基础解系仅由n-r(A)=1个解向量组成. 从而β1，β2线性相关.